암호 해시 함수 : 정보 보안 - 암호학

https://youtu.be/KlAPDaCC_eU?si=yDrBDVDvGcLZ0DI-

 

 

암호 해시 함수, 영어로는 Cryptographic Hash function 이다.

 

A → B 로 전송되는 메세지를 공격자가 interrupt 했을 때 메세지를 읽지 못하도록 하거나 메세지를 변조하지 못하도록 하는 것을 기밀성과 무결성이라고 한다.

아니면 A 와 상관없이 B 에게 공격자가 메세지를 위조하여 보낼 수도 있다. 이때 필요한 것이 메세지 인증이다.

 

즉 위의 예시에서처럼

 

보안 요구사항

• 기밀성 (Confidentiality)
  • 암호
• 메세지 무결성 (integrity) & 메세지 인증 (authentication)
  • HMAC(keyed Hash)
  • 전자 서명
  • 인증 암호 (authentication encryption = 인증 + 암호화)

그 중 Hash 를 좀 더 자세히 살펴보면,

 

암호 해시 함수의 응용

• 해시 함수는 암호학에서 중요한 도구로서 여러가지 목적으로 사용된다.
  • 메세지 인증 코드 (MAC)
  • 전자 서명 (digital signature)
  • 키 생성 (key derivation)
  • (암호, 일반 난수는 아니구) 난수 생성 (random number generation) 등등
• 주의할 점
  • 해시 함수는 암호, 복호를 위한 알고리즘이 아니다.
  • 따라서 암호 알고리즘과 같은 암호화 키(key) 는 없다.

 

(일반적인) 해시 함수란?

• 목적
  • 입력값보다 더 작은 길이의 출력값을 만들어낸다.
  • 출력값은 입력값이 갖는 특성을 그대로 가지고 있다.
  • 예를 들면,
    • 해시함수 H(x) 가 입력값 x 의 각 숫자 합으로 출력값을 만든다고 할 때
    • x = 583729847 이면 → H(x) = 53 (5+8+3+7+2+9+8+4+7) 이다.

 

해시 함수 예시

(컴퓨터 네트워크) 데이터 통신에서 에러 검출 코드 (Error Correction Code) 를 만드는데 해시 를 많이 사용한다.

ex) CRC, CheckSum

 

메세지 → [H] → 에러 검출 코드

를 이용해 에러 검출 코드를 메세지 뒤에 붙여서 같이 보낸다. 이 목적은 메세지의 에러(바뀌었는지 등) 를 확인하기 위해서이다.

왜 암호에서 해시 함수가 필요한가?

만약 송신자 A 가 메세지 M(을 보내면서) 에 대해 서명을 한다고 하자,

 

서명 S= sign(M)_K-A, 이때 K_A 는 A 의 개인 key. 이를 통해 전자서명 S을 만든다.

이후 M 과 S 를 B 에게 보낸다.

B 는 전자서명값 S 를 이용해 M 이 제대로 되는지 증명한다. M = verify(S)_K+A

이 때 A 의 공개키 K+A 를 이용해 계산한다.

 

https://youtu.be/KlAPDaCC_eU?si=yDrBDVDvGcLZ0DI-

 

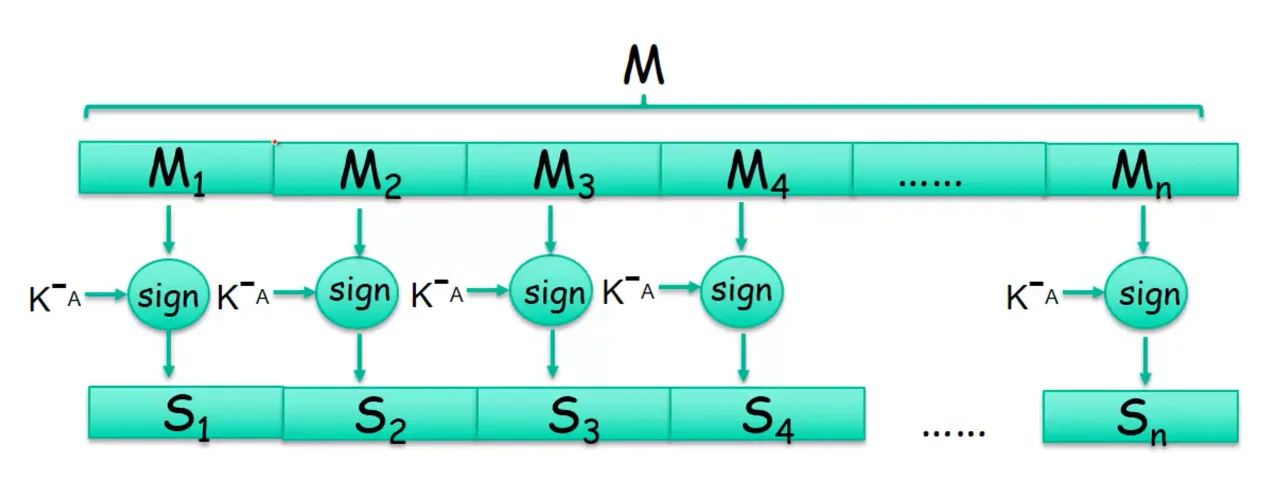
근데 이때 위 그림처럼 블록암호를 사용하기 때문에 메세지를 블록 단위로 자른다.

그러면 M 와 같은 길이의 S 를 추가해서 보내야 하는데 너무 낭비가 심하다.

 

그러므로 해시를 사용한다.

 

https://youtu.be/KlAPDaCC_eU?si=yDrBDVDvGcLZ0DI-

 

하지만 A 가 M 대신 M 의 해시값 H(M) 에 대해 서명을 해서 보낸다면 훨씬 간단하게 작업을 처리할 수 있다.

왜냐하면 H(M) 이 M 보다 훨씬 짧은 길이를 가지기 때문이다.

 

암호 해시 함수의 요구사항

→ 암호에서는 일반 해시 함수를 사용할 수는 없고 특별한 해시 함수를 사용한다.

 

A 는 S 를 계산한다. S= sign(h(M))_K-A

A 는 (M, S) 를 B 에게 보낸다.

B 는 메세지를 인증한다. h(M)= verify(S)_K+A,

 

• H 가 가져야 하는 특성
  • 만약 공격자가 h(M) = h(M’) 를 만족하는 M’ 를 찾아낸다면 B 는 M 메세지가 M’ 로 변조된 것을 알 수 없다.
  • 그래서 암호에서 사용되는 해시함수 h 는 M’ 를 찾는 것이 매우 매우 어려워야 한다.!!

 

암호 해시 함수는 다음의 성질을 가져야 한다.

• 입력 메세지는 임의의(정해진) 길이를 가진다.
• 메세지 압축 : 출력값(해시값) 은 고정된 짧은 길이여야 함
• 계산 효율 : 임의의 x 에 대해 h(x) 를 용이하게 계산할 수 있어야 한다.
• 단방향 : 임의의 y 에 대해 h(x)=y 를 만족하는 x 를 찾는 것은 거의 불가능(infeasible) 해야한다.
• 약한 충돌 방지 : 임의의 x 와 h(x) 가 주어졌을 때 h(x)=h(y) 인 y (x not= y) 를 찾는 것은 거의 불가능 해야한다.
• 강한 충돌 방지 : h(x)=h(y) 인 x 와 y (x not= y) 를 찾는 것은 거의 불가능 해야 한다.

 

** 충돌이란 : 출력값은 입력값보다 길이가 작으므로 당연히 입력값 집합이 출력값 집합보다 클 수 밖에 없다. 그래서 동일한 출력값을 가지는 입력값이 있을 수 밖에 없다. 이를 collision 충돌이라 한다.

 

그렇다면 충돌이 거의 불가능 하려면 출력값의 길이가 얼마나 되어야 하는가?

 

→ Pre-Birthday problem

 

• N 명의 사람이 한 교실에 있을 때
• 나와 같은 생일을 가지는 사람이 적어도 한명 있을 확률이 1/2 이상이 되려면 N 은 얼마가 되어야하는가?
  • $\frac{1}{2} =1-(\frac{364}{365})^{N-1}$
  • N = 253

 

생일 문제

https://youtu.be/KlAPDaCC_eU?si=yDrBDVDvGcLZ0DI-

 

→ 다시 강한 충돌 방지로 돌아와서,

 

강한 충돌 방지 ( Strong collision Resistance)

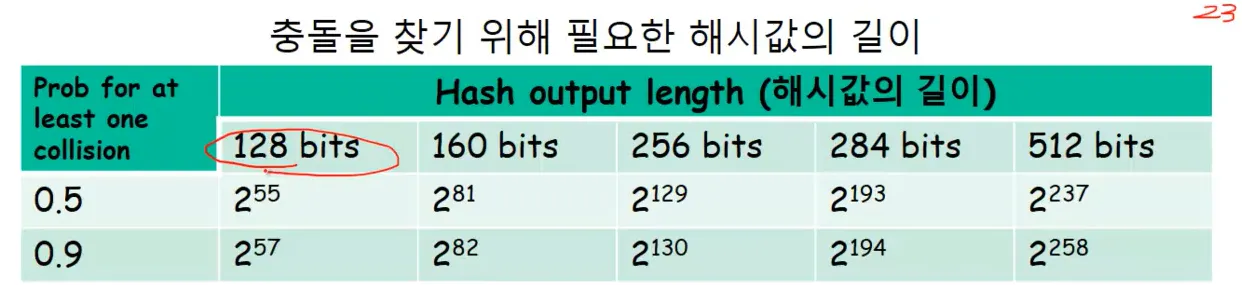
h(x) 가 N bit 라면, 2^N 개의 해시값이 나올 수 있다.

• 생일 문제의 365 에 해당

따라서 $\sqrt{2^{N}}$ = 2^{N/2} 만큼 비교하면 동일한 해시값이 만들어질 확률이 1/2 가 된다.

 

https://youtu.be/KlAPDaCC_eU?si=paJHnu7pIegK7hTq

 

안전한 해시 함수의 설계

• 많은 비암호 해시 함수 (ex) Cyclic Redundency Check) 가 존재하지만 모두 안전하지 않다.
• 요구되는 특성 : 눈사태 효과 (Avalanche effect)
  • 입력값은 1bit 다르더라도 출력값은 반 이상의 bit 가 달라야한다.
  • 따라서 암호 해시 함수는 여러번의 섞는 과정이 필요. (round)
• 안전과 속도
  • 여러 번 섞는 과정으로 Avalanche effect를 만듦
  • 하지만 적절하게 섞는 과정이 필요하다.
• 블록 암호 알고리즘의 설계와 비슷하다.

 

https://youtu.be/KlAPDaCC_eU?si=paJHnu7pIegK7hTq