Roformer: Enhanced Transformer with Rotary Positon Embedding
https://arxiv.org/pdf/2104.09864.pdf
에서 처음 제안된 방법이다.
Abstract
기존의 PE 는 트랜스포머에서 제안된 방법으로, 시퀀스 내의 토큰을 attention 만으로는 순서 정보를 줄 수 없어서 사용한 효과적인 방법. 이후 다양한 PE 방법이 나왔는데,
이 논문에서는 새로운 Rotary Position Embedding(RoPE) 제안한다.
RoPE 는 rotation 행렬을 이용하여 절대 위치를 인코딩하고, self-attention 식에서 relative position dependency (상대 위치 의존성) 정보를 더해준다.
이를 통해 long text classification 벤치마크를 평가한다.
Introduction
기존 PE 방법들이 왜 적합하지 않는지?
Background
2.1. Preliminary
$S_{N} = \{w_i\}^{N}_{i=1}$ : N개 인풋 토큰의 시퀀스.
$E_{N} = \{x_{i}\}^{N}_{i=1}$ : 위에 대한 PE 가 적용되지 않은 word embedding 은 E 이다.
$x_{i} ∈ R^{d}$ : 이때 d는 임베딩 디멘션 크기.
Self 어텐션은 처음에 워드 임베딩에 PE 를 추가하고 key query value representation 을 만든다.

q_m, k_n, v_n : m 번째, n 번째 위치 / 여기서 $f_q, f_k, f_v$ 는 위치 정보를 더해주는 함수를 의미.

이후 self attention 적용.
PE History : 1. Absolute position embedding (절대 위치 임베딩)
Attention is all you need 이후 다양한 방법이 나왔지만 가장 대표적인 방법인 sinusoidal 방식만 설명하겠다.
n번째위치를 나타내기위한 n에 대한 함수로 계산하는 방식.
절대적 위치 기반 이더라도 토큰간의 상대적 관계가 유지되어야 한다.
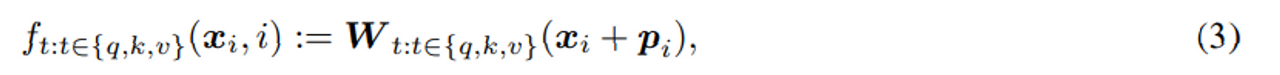
절대 위치 임베딩은 위와 같이 기존 인풋 시퀀스에 포지션 정보를 더하고, wright 를 곱해 key query value 생성한다.
p는 토큰 x 에 위치에 따른 d 디멘션 벡터이고, 이때 L은 max seq len 을 가진다.

이후 연구에서는 trainable vector p 에 대한 방법 제안도 나왔다.
PE History : 2. Relative position embedding (상대 위치 임베딩/RPE)
Relative PE는 포지션 정보를 트랜스포머 내부 어텐션 에서 key-query matching 행렬에 더해주는 방식.
즉, key의 i번째 요소와 query의 j 번째 요소 사이 dot product (어텐션에서) 한 후 이 (i-j) 값을 기반으로 learnable 한 lookup 표로부터 PE를 가져와 더해준다.
이 경우에는 특정 조건의 정해진 sinusoidal PE table을 계산하는 함수가 필요 없다는 장점이 있다.
1. shaw 의 연구
Radford 처럼 훈련을 통해 relative PE정보 p를 얻지만 포지션 정보를 아래와 같이 k와 v에만 더해준다.
왜냐하면 query 를 relative 거리의 기준점으로 삼기 위해서이다.

1번 식을 위와 같이 세팅한다.
이 때 $p˜^{k}{r} , p˜^{v}{r}$ 는 학습가능한 relative position 임베딩이다.
$r = clip(m − n, r_{min}, r_{max})$
r은 위치 m과 n 사이의 상대거리를 말한다.
Clip 식이 포지션 m과 n사이의 relative distance 를 나타낸다. (m 을 원점으로 정의)
이를 통해 상대거리를 clip하여 일정 거리 이상은 정확한 상대거리는 사용하지 않는다.

$A_{m, n} = (W_{q}x_{m})^{T}(W_{k}(x_{n}+p_{n}))$
이렇게 키와 밸류에만 positon 인코딩을 더하는 방식이다. 위는 6 식을 정리해본 것이다.
A_m,n 은 attention score 이다.
위 식에서 첫 번째 항부터 context-to- context, c-to-positon, p-to-c, p-to-p 라고 말할 수 있다.
여기서 $p_{n}$ 부분이 $R_{m-n}$ learned position 으로 대체된다.
쿼리의 위치를 기준점처럼 사용하기 때문에 식에서 없앤 것이다.
2. Dai (Transformer-XL 연구)
Shaw 연구에서는 query 에 positon 를 빼지만 transformer-xl 이후 연구 부터는 value 에도 position 정보를 주입하지 않는다.
그래서 $A_{m, n} = x_{m}^{T}W_{q}^{T}W_{k}x_{n}+x_{m}^{T}W_{q}^{T}W_{k}p_{n}$ 가 최종 식이 된다.
(이렇게 빠진 항들은 이후 논문에서 문제 제기가 된다.)

6 식에서 $p_{m}$ 을 learned position 인 u, v 로 대체하고 위의 $R_{m-n}$ 은 sinusoid position 으로 대체한다.
여기서 sinusoid 정보는 그냥 n-m 값을 attention-is-all-you-need 에 있는 sin cos 포지션 인코딩 식에 대입한 값이다.
주된 아이디어는 3번째, 4번째 term 에 있는 절대 포지션 정 p_m 을 퀴리 포지션과 독립적인 학습 가능한 파라미터 u v 로 대체하는것, 그리고 절대 포지션 임베딩 pn을 sinusoid-encoded relative counterpart(상대 포지션 임베딩) p~_{m−n} 로 대체하는 것이다.
즉, 여기에서도 query 를 기준점으로 사용하는 방식은 그대로 차용되어 position m 에 따라 다른 거리를 가지던 PE 가 결정되었다.
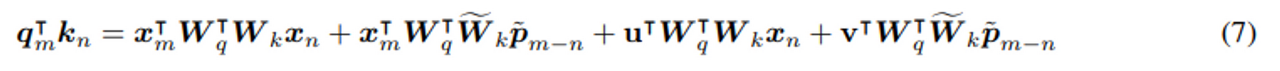
결론은 위와 같은 식이다.
~ Tilda 는 그냥 position에 대한 행렬 이라는 뜻. (강조하는 의미로 사용)
3. T5 연구
이후 연구는 f_{v}(x_{j}) := W_{v}x_{j} 를 세팅함으로서 Value term 의 포지션 정보가 제거하고 어텐션 웨이트 에 상대 포지션 정보 를 인코딩한다. 하지만 2020 연구(T5)에서 이를 6번식을 밑 과 같이 바꾸었다.

b_{i,j} 는 학습가능한 bias 이다. =즉, content-to-content term 이외의 나머지 3개 항은 전부 (모델이 알아서 학습하도록) 학습가능한 항으로 바꿔버림 → 그래서 Efficient Transformer 에서는 적용불가
⇒ 이로서 RPE 가 Efficient Transformer 에 적용 가능한 지의 여부가 매우 중요한 점임을 알 수 있다.
4. TUPE (Transformer with Untied Positional Encoding)
다시 6 번 식을 가져오자.

다시 말하지만 위의 식은 4종류의 상관 관계가 나타난다고 할 수 있다.
첫째 항부터 순서대로 토큰-토큰, 토큰-포지션, 포지션-토큰, 포지션-포지션이다.
여기에서는 6식의 각 term 을 조사하여 중간 2개 term 에 대해 absolute position과 word 사이의 correlation 에 대해 거의 uniform 하다는 사실을 알았다. 그래서 불필요하다고 제거함.
word 나 position 쌍에 다른 projection 행렬을 사용하는 방식을 제안한다.
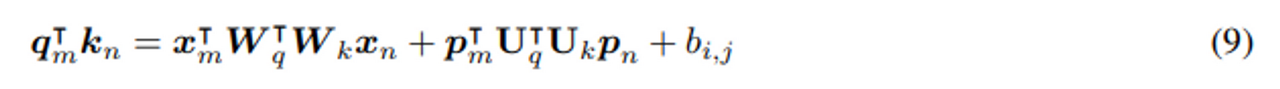
위 식처럼 content-to-content 와 position-to-position 이 같은 파라미터를 공유하지 말아야 한다고 주장. 이 논문에서도 pos-to-pos 는 없애고 나머지 항에 대해 unify 하여 위 논문 연구를 적용하여 제안. / → 즉 4가지 정보에 대해 똑같이 W*W^t weight 를 사용하는데 이는 적절하지 않다는 것.
5. 마지막으로 DeBERTa (Decoding -Enhanced BERT with dis-entangled attention)
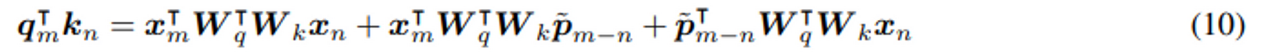
pos-to-pos 항은 의미가 없다고 주장한다.
4번 연구는 Pos-to-content 텀을 삭제했지만, 이 항도 매우 중요하다고 주장한다.
b 와 c 항의 absolute PE 를 RPE 로 교체한다.
** 이게 제일 성능이 좋았다.
⇒ 어쨋든 지금까지의 방법들은 전부 relative position 정보를 additive 한 방식으로 사용함을 알 수 있다.
Method
Rotary embedding은 GPT-J 에서 사용해서 유명해진 방법이라고 한다.
매 레이어마다 PE값을 해준다.
3.1 formulation
상대 PE 정보를 포함 위해서는 q와 k 사이의 내적이 g 함수를 통해 수식화되어야 한다.
이 함수는 워드 임베딩 x_m , x_n 과 그들의 상대 위치인 m-n 만을 인풋으로 가진다.
즉 우리는 내적이 상대적인 위치정보만 인코딩했으면 좋겠다는 것이다.
다음 11식이다.
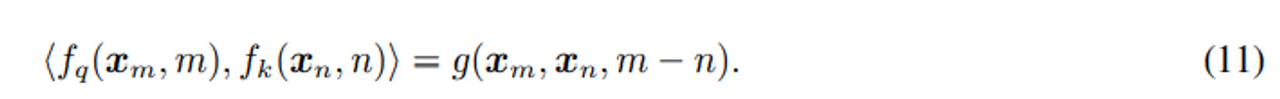
궁극적인 목적은 이전에 언급한 relation 에 맞는 f_k와 f_q 함수를 푸는 equivalent한 인코딩방법을 얻고 싶은 것.
그래서 상대 포지션 정보를 포함하는 새로운 내적 함수 g 를 수식화해야한다.
= 이것이 논문에서 풀어야하는 솔루션이다.
💡 Affine transform 은 w x + b weight와 bias 식으로 이루어진 transform 이다.
** 복소수와 극형식 변환 개념
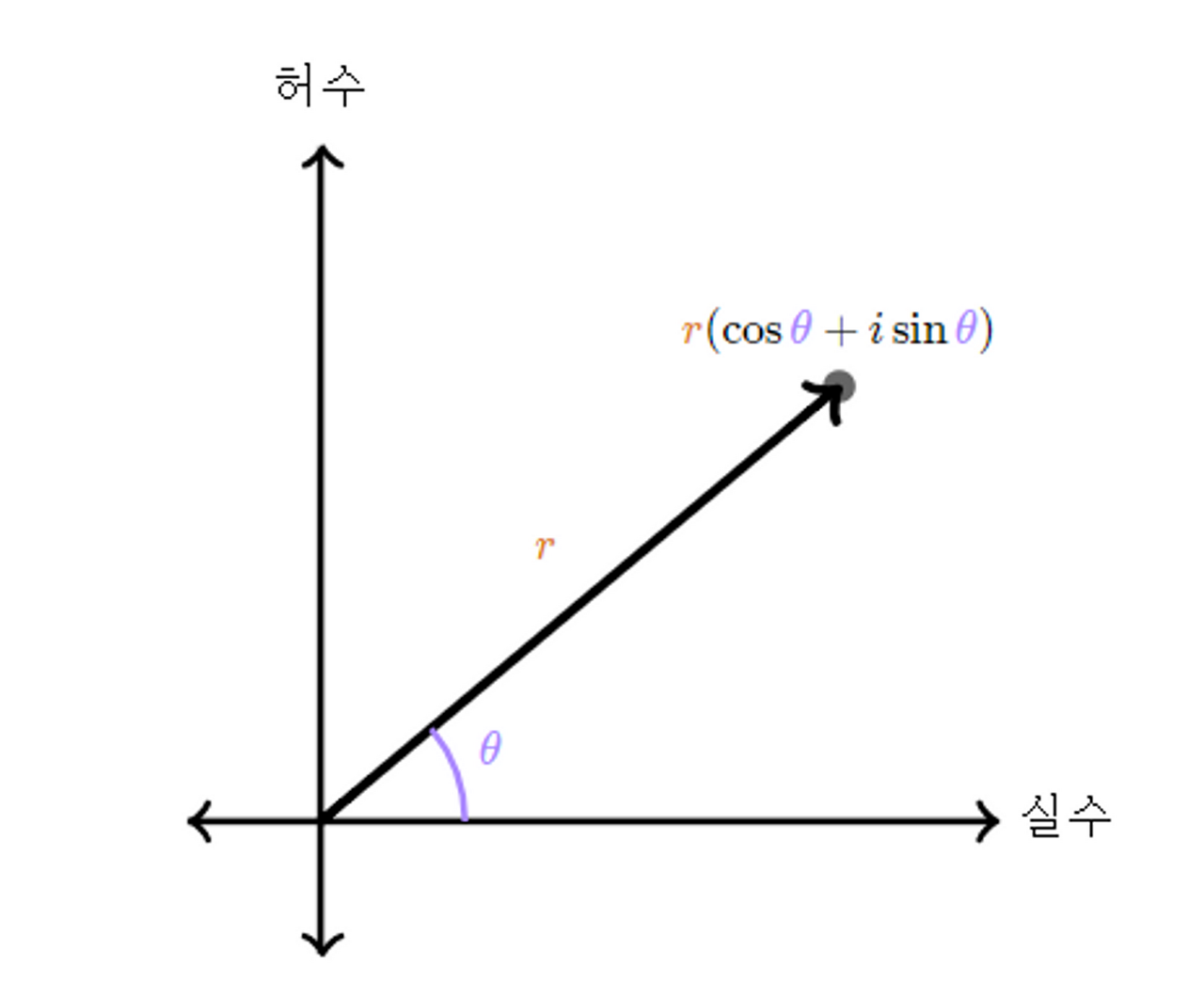
각도 $\theta$ (angular) 와 길이 r (radical) 은
$r cos \theta + j*rsin\theta$
복소수 형식으로 표현할 수 있다.
3.2 메소드 설명
Dimension d=2 일 때 2d 벡터와 그의 complex form 이다.
** 결론: 워드임베딩 벡터를 complex(복소수) 꼴로 변환시킨 후 이를 rotation 한다. 그렇게 되면 word embedding 의 절대적인 값이 바뀐다.
Self attention에서 사용하는 ‘내적’ 은 내적 하는 벡터 사이 각도에 대한 함수이므로 $ab = |a||b|cos\theta$ 두 벡터에 대한 상대 거리 (각도의 차이 m-n)가 보존될 수 있다.
→ 그래서 오히려 (이전에 사용해온) 절대 포지션 정보를 더해주는 방식은 효율적이지 못하다는 것.
1. 2D case
이 논문에서의 11번식의 솔루션은 12번 식이다.
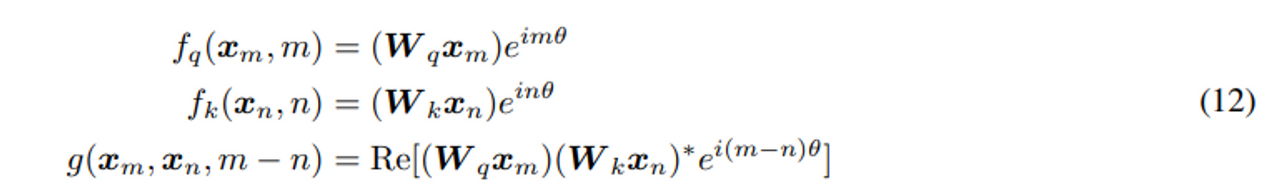
💡 $<x, y> =\sum Re(x_i· y^∗_i)$ : 이를 내적 정의라고 한다.
<: 브라, > : 켓 → < 는 > 와 반대이므로 Transpose 를 뜻한다고 한다
Re[*] 는 복소수 의 real 부분이다.
(W_k x_n)* 는 (W_k x_n)의 conjugate(a+bi 가 있을 때, a-bi 형태) form 이다.
$\theta \in R$ 는 non-zero constant(상수) 의 preset(디폴트 값 set) 이다.
더 나아가서 우리는 $f_\{q, k \}$ 를 행렬 곱으로 나타낼 수 있다.
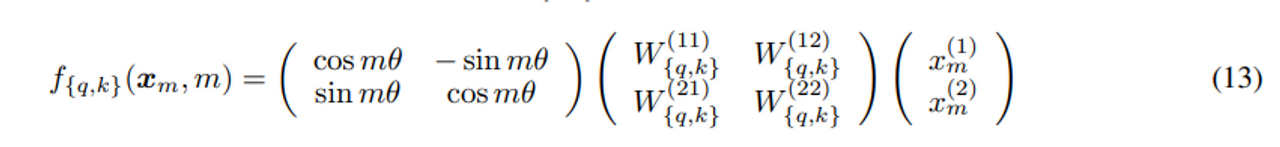
위 식의 RHS 의 1번째 cos sin 행렬은 회전변환(rotation matrix)을 나타냄.
RHS 의 2번째 행렬은 affine Transformer 행렬이다. → 위에서 말한 것 처럼 key query W 행렬
$(x^{(1)}m , x^{(2)}{m})$ 은 $x_m$ (토큰)의 2d 좌표 를 나타낸다.
relative Positon Embedding : affine-transformed 워드 임베딩 벡터 를 포지션 인덱스로 weighted 한 (일정량의) 앵글을 이용해 단순히 회전시켜 rotary PE를 표현할 수 있다.
** rotary = rotation 회전이라는 뜻
2. General form
2d를 짝수 d에 대해 일반화할 수 있다. (d 가 짝수여야 한다는 조건을 가진다.)
d를 d/2 의 sub-space로 나누고 내적의 linearity 장점을 통해 f{q,k}를 14식으로 합친다.
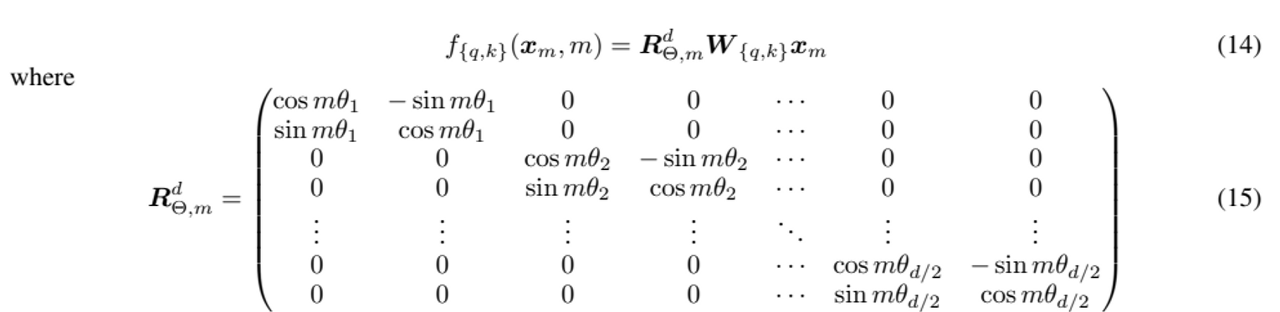
하지만 (당신도 느꼇다시피) 위 식은 회전변환의 general form 은 아니다.
서로 다른 index 에 대해 회전변환을 적용하기 위해 d/2 개의 2차원 회전변환식을 sparse 하게 모아놓은 꼴이다.
이는 일반 Transformer 포지션 인코딩인 4번 식과 비슷하다.

위는 각 token 의 인덱스에 따라 sinusoidal 함수 형태가 변한다.
RoPE 는 토큰의 인덱스에 따라 다른 회전변환의 함수를 사용한다.
Rotary 행렬에는 pre-defined parameters 인 $Θ = \{θ_{i} = 10000^{−2(i−1)/d}, \space i ∈ [1, 2, ..., d/2]\}$ 가 있다.
RoPE 를 식2의 셀프 어텐션에 적용하면 16식과 같이 된다.

위에서 $R^{d}{Θ,n−m} = (R^{d}{Θ,m})^{T} R^{d}_{Θ,n}$ .
이때 $R^{d}_{Θ}$ 은 orthogonal 행렬이고, PE 할 때 stability 를 주는 역할이다.
근데 이 친구의 sparsity 때문에 식 16 처럼 행렬곱을 직접 적용하는 것은 계산적으로 효율적이지 않다.
이전 연구들에서 사용된 (식 3 - 10) position embedding 을 더하는 방법과 다르게, 이 논문의 방법은 multiplicative 하다. (곱하기로 이루어진다)
게다가 RoPE 는 더하기로 term(항) 자체를 변화시키는 대신 상대적 위치 정보를 rotation 행렬 product을 이용해 통합한다.
실제 구현에서는 이렇게 sparse 하면 매우 비효율적이기 때문에 논문 appendix B 부분처럼 구현하였다.
cos 과 sin 을 나눠서 계산한다. (구현이 쉽다는 장점이 있다.)

밑에 그림은 RoPE를 설명한다.

** 결론: 워드임베딩 벡터를 complex(복소수) 꼴로 변환시킨 후 이를 rotation 한다. 그렇게 되면 word embedding 의 절대적인 값이 바뀐다.
Self attention에서 사용하는 ‘내적’ 은 내적 하는 벡터 사이 각도에 대한 함수이므로 두 벡터에 대한 상대 거리가 보존될 수 있다.
→ 그래서 오히려 (이전에 사용해온) 절대 포지션 정보를 더해주는 방식은 효율적이지 못하다는 것.
3.3. 특징 (위에서 말한 장점)
long term decay :

Long decay 에서 위의 그래프에서 y축의 Relative upper bound (이 부분은 attention score 라고 생각하면 될거 같다)
Attention is all you need과 똑같이 theta 를 $θ_{i} = 10000^{−2i/d}$ 로 설정한다.
이 설정이 long term decay 특성이라는 것은 Section (3.4.3) 에서 증명된다. = 이 의미는 relative position 이 증가하면 내적 값이 (decay 부식, 떨어짐) 떨어짐을 의미한다.
이 특성은 서로 긴 relative distance 를 가지는 토큰 쌍이 더 적은 connection 을 가져야 한다는 직관과 일치한다.
Linear attention 에서의 RoPE :
이 논문에서는 오리지널 attention 메타니즘이 아닌 (다른 트랜스포머 연구 논문에서 사용한) linear attention을 사용하였는데 여기에 적용할 수 있는 방안까지 함께 제안하였다. = 그래서 Efficient Transformer 에도 적용가능.
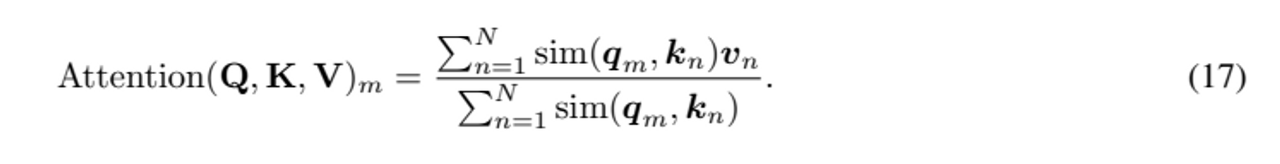
self-attention 은 위의 식처럼 더 일반적인 식으로 표현할 수 있다.
attention is all you need 에서의 (오리지널) 어텐션 식은 밑과 같다. $sim(q_{m}, k_{n}) = exp(q^{T}{m}k{n}/√d)$
오리지널 어텐션은 모든 key query 의 내적을 다 구해야 한다. 이 계산 복잡도는 quadratic 으로, O(N^{2}) 이다.
(이를 해결하기 위해 밑의 개념을 도입한 듯.)

위는 다른 논문에서 제안한 linear attention 식이다.
** 한 가지 이상한 점 : 리니어 어텐션에서는 더하는 position 인코딩을 못하는건 아니다. 하지만 왜 RoPE에서는 자기네는 곱하기라서 적용이 가능하다고 하는지 모르겟다.
💡 여기서 $\phi$ 는 커널(kernel) 이다. 커널 트릭은 머신러닝 관점에서 pTp* 이 WTx 에 치환할 수 있다는 점으로 사용 가능.
커널함수×커널함수=커널함수 임은 이미 증명되어있다.
위 식에서 $φ(·), ϕ(·)$ 는 대게 non-negative 함수이다.
그 논문에서는 $φ(x) = ϕ(x) = elu(x)+ 1$ 라고 제안하고, 행렬곱의 associative 특성을 이용하여 key 와 value 의 곱을 먼저 계산한다. (? 이해가 안된다. 당신도 그렇다면 https://arxiv.org/pdf/2006.16236.pdf 참조.)
softmax 함수는 내적을 하기 전에 key 와 query 를 각각 normalize 하는 데에 사용한다.
이는 $φ(q_{i}) = softmax(q_{i}) \space and \space φ(k_{j}) = exp(k_{j})$ 와 같다.
이 섹션에서는 RoPE 와 식 18 번을 결합하는 데에 초점을 둔다.
RoPE 는 위치정보를 hidden representaion 의 norm 을 변화시키지 않는 rotation을 이용해서 주기 때문에 RoPE 와 linear 어텐션을 non-negative 함수 결과값에 회전 행렬을 곱해줘서 합칠 수 있다.

주목할 점은 0 으로 나눌 위험을 피하기 위해 분모를 변하지 않도록 하고, 분자의 합이 negative 가 포함될 수 있다는 것이다.
위 식 19번에서 각 value v_{i} 의 weight 가 엄격하게 probabilistic normalized 되지 않았음에도 불구하고 우리는 이 계산이 value 의 importance 를 모델링할 수 있다고 주장한다.
** RoPE 는 이후 long sequence 에 대한 position 정보 에 대해 매우 많은 adaptation 이 생긴다.
그 중 하나가 RoPE NTK scaling.
'LLM 관련 논문 정리' 카테고리의 다른 글
| Few-Shot Parameter-Efficient Fine-Tuning is Better and Cheaper than In-Context Learning (NIPS, 2208) (0) | 2023.09.30 |
|---|---|
| PEFT (parameter-efficient fine tuning) 정리 (0) | 2023.09.18 |
| InstructGPT 상세 리뷰 (0) | 2023.08.30 |
| NTK-aware dynamic interpolation (0) | 2023.08.21 |
| LoRA (Low-Rank Adaptation of Large Language Models) (0) | 2023.08.10 |
